La sezione aurea e la celebre sequenza di numeri ad essa correlata racchiudono numerose proprietà algebriche e geometriche che hanno da sempre affascinato studiosi, in tempi remoti e recenti. La sezione aurea è a tale punto presente nella realtà fisica da investire l’intero creato e da essere definita come la proporzione divina. Per questa sua peculiarità è stata applicata in vari ambiti e discipline, non ultima la musica.
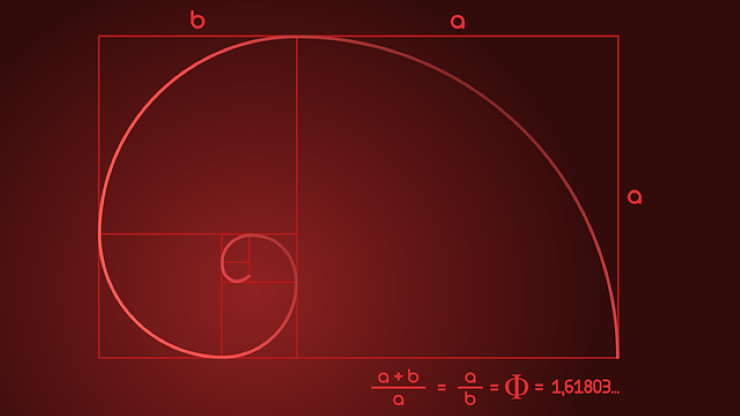
La sequenza di Fibonacci consiste in una successione di numeri interi positivi in cui ciascun numero è la somma dei due numeri precedenti.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610… fino all’infinito
La sequenza di Fibonacci è strettamente connessa con la cosiddetta sezione aurea, in quanto il numero che la individua è dato dal rapporto tra due numeri vicini nella successione. Quanto più i numeri considerati sono alti, tanto più il valore ottenuto sarà approssimato a 1,618, ovvero il numero più discusso e più enigmatico del mondo. Esso può essere individuato in ogni aspetto della natura, dalla botanica all’anatomia, tanto da essere considerato come una firma del creatore stesso. Per questo motivo il numero Φ (=phi) è definito il numero della proporzione divina.
Tale numero e la sequenza di Fibonacci sono stati utilizzati anche nell'arte, nell’architettura e nella musica. Ricorrono nelle piramidi, nel Partenone di Atene e in numerose rappresentazioni scultoree e pittoriche, di queste ultime, ne è un esempio la Gioconda di Leonardo da Vinci.
La sequenza di Fibonacci gioca un ruolo importante anche nell'armonia e nelle scale musicali occidentali. A questo proposito, basta considerare che:
un'ottava al pianoforte è composta da 13 note, otto sono tasti bianchi e cinque sono tasti neri;
una scala è composta da otto note, di cui la terza e la quinta creano la base di un accordo;
in una scala, la nota dominante è la quinta nota, che è anche l'ottava nota di tutte le 13 note che compongono l'ottava.
Osservando questo elenco, emergono delle ricorrenze familiari: otto diviso 13 equivale a 0,61538, ancora una volta il rapporto aureo, inoltre, quelli appena citati sono tutti i numeri della successione individuata dal matematico italiano: 3, 5, 8, 13.
Del resto, basta vedere una tastiera di pianoforte per ritrovarne una rappresentazione chiara ed evidente.

Nel corso della storia non sono mancati compositori che hanno fatto riferimento consapevole alla serie numerica fibonacciana e alla sezione aurea per comporre la loro musica.
Mozart, ad esempio, ha basato molte delle sue opere sulla sezione aurea, in particolare le sue sonate per pianoforte.
La sonata tradizionale era strutturata in due parti: esposizione, dove veniva introdotto il tema musicale; sviluppo e ricapitolazione, dove il tema veniva sviluppato e ripetuto.
Mozart ha concepito le sue sonate per pianoforte in modo che il numero di battute nello sviluppo e nella ricapitolazione, diviso per il numero di battute nell'esposizione, fosse pari a circa 1,618.
Prendendo, ad esempio, il primo movimento della Sonata per pianoforte n. 1 in Do maggiore del genio salisburghese, si puo constatare che l' esposizione è composta da 38 battute e lo sviluppo e la ricapitolazione da 62. Il primo movimento nel suo insieme è composto da 100 battute. 62 diviso 38 è uguale a 1,63 (approssimativamente la sezione aurea).
Proporzioni auree sono rintracciabili chiaramente anche in Bach, ad esempio nell’Arte della fuga, o nella Quinta sinfonia di Beethoven, ma anche in Bartók, Debussy, Schubert e Satie (per citarne alcuni).
Non solo in ambito classico, anche la musica rock è ricorsa alla Sequenza di Fibonacci, come nel caso dei Genesis e della loro Firth of Fifth, in cui troviamo tre assoli che hanno lunghezze di 13, 34 e 55 battute, anche questi numeri facenti parte della celebre serie.
Sempre in ambito rock, si possono citare anche i Deep Purple e il loro brano Child in Time, interamente concepito secondo il rapporto tra i numeri 8 e 5 e termini consecutivi della sequenza di Fibonacci. Ma anche l’album Octavarium dei Dream Theater e il pezzo Lateralus dei Tool sono concepiti sulle sequenze fibonacciane. L’uso di questi rapporti numerici nella composizione musicale attraversa, dunque, i secoli e i generi, anche se nessuno è mai stato in grado di spiegare esattamente il perché funzioni così bene.
Antonio Stradivari, acclamato maestro della liuteria, ha realizzato alcuni dei violini più belli e sonori esistenti, servendosi anch'egli della Sequenza di Fibonacci e della Sezione Aurea per costruirli.
La sezione aurea può essere rintracciata in tutti i suoi violini dividendo le lunghezze di parti specifiche dei suoi strumenti. Secondo alcuni questo è uno dei motivi per cui suonano così bene.
Oltre ad essere utilizzato per fabbricare violini, il rapporto aureo che deriva dalla sequenza di Fibonacci viene utilizzato anche per i bocchini per sassofono, nei cavi degli altoparlanti e persino nella progettazione acustica di alcune cattedrali.